Online Convex Optmization with Switching Costs

Recently in COLT 2012, an excellent paper entitled Unified Algorithms for Online Learning and Competitive Analysis makes a progress towards unifying the algorithms from two different communities of online leaning and competitive analysis. There is a few crucial differences in assumptions and goals of these two frameworks for online decision making which is the reason why there has not been much research on connecting the two. First, in competitive analysis (a.k.a online algorithms) there is a state concept which is usually modeled as switching or movement cost. Second, in online algorithms one assumes that the cost vector for next round is known to the algorithm to make the decision; in contrast, in online learning, the decision maker first makes the decision for next round and after that observes the cost vector. One interesting questions in connecting these two setting would be adding the switching cost to the regret incurred by the online learner. More specifically, one may consider the 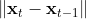as the movement cost at round t. Obviously, the decision maker needs to consider the switching cost in his decision to minimize it. Having this formulation, the learner competes with the best offline decision maker with bounded switching cost. When the bound on switching cost is in terms of number of rounds T, then we recover the standard setting of online learning. I will post more about this problem and some solutions soon, hopefully :-)