Regret Bound by Variation for Online Convex Optimization

Recently, we tried to find regret bounds by variation for general Online Convex Optimization problem. If one goes through the Chapter 2 of Prediction, Learning, and Games, he/she can easily find three different ways to express the regret bound: in terms of the number of rounds T, loss of the best expert, and variation of cost vectors. In Extracting certainty from uncertainty: regret bounded by variation in costs , the authors extend the result to online linear optimization and showed that the regret of online linear optimization can be bounded by the total variation of the cost vectors. In our work, we extended this result to general OCO. We first analyze the limitations of the algorithm in Extracting certainty from uncertainty: regret bounded by variation in costs when applied it to online convex optimization. We then present two algorithms for online convex optimization whose regrets are bounded by the variation of cost functions. We finally consider the bandit setting, and present a randomized algorithm for online bandit convex optimization with a variation-based regret bound. We show that the regret bound for online bandit convex optimization is optimal when the variation of cost functions is independent of the number of trials.

Online Convex Optimization without Projection

In this post I would like to briefly discuss our recent work in Online Convex Optimization (OCO) namely OCO with Long Term Constraints. Classical gradient descent optimization techniques usually require a projection step in each iteration, in order to get back to the feasible domain. Although for simple convex domains like Eculidain ball and simplex, this is a well studied problem and there exists efficient algorithms, however; for a variety of applications, this is a non-trivial and computationally burdensome step. One prominent example is semide nite optimization, where the projection of an arbitrary symmetric matrix back to the PSD matrices requires the computation of a complete eigenvalue-decomposition. Comparing this to the linear time update of first order gradient methods, it makes more sense to resolve this problem. In OCO, this is more crucial since the running time of each step supposed to be more efficient. We tackled this problem by posing a new OCO problem. The intuition is to replace the complex convex domain with simpler one with efficient projection algorithm and see how this process affects the general performance of the algorithm. The solution we proposed seems interesting in its own way; leaving some open problems needs through investigation.

COLT 2011 Accepted Papers

The list of accepted papers for COLT 2011 are available here. I will update this post by adding related papers to my own research soon

Online Learning with a Partially Observable Future Cost

The main idea in proving regret bound for the Follow the Perturbed Leader (FPL) algorithm is as follows: first, we define the hypothetical leader which knows the future cost vector before prediction on round 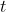which attains zero regret. Then we can prove that by adding some perturbation to the current cumulative cost vectors till time 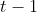the Player gets regret bound. Now the question is that if we have some partial information about future cost or we are allowed to query some information about the next round's cost, can we design algorithms with improved regret bounds. This problem is tackled down in two recent papers. In Online Learning with Prior Knowledge the authors proposed an algorithm which utilize such information as a kind of prior information. Recently in Online Learning with Queries a variant of Weighted Majority Algorithm with capability of querying limited information about the future cost vector is proposed.

No Free Experts, Hedging on Cost

Consider the following setting for learning from expert advice. In each round of the game between Player and Adversary, the player can ask for experts' suggestions but by paying some amount of money determined by each expert at the beginning of the round. In other words, at the beginning of each trial, the Player gets a cost vector which determines the cost of querying each expert for that round. Also let assume that Player has a budget constraint which would be for each round or long term constraint defined for all rounds. The goal of Player is to attain nontrivial regret bound under the budget constraint. Formally the Player tries to minimize and simultaneously satisfies the constraint .

The mentioned constraint is a long term constraint and we can alternatively define round based constraint as:.