Online Convex Optmization with Switching Costs

Recently in COLT 2012, an excellent paper entitled Unified Algorithms for Online Learning and Competitive Analysis makes a progress towards unifying the algorithms from two different communities of online leaning and competitive analysis. There is a few crucial differences in assumptions and goals of these two frameworks for online decision making which is the reason why there has not been much research on connecting the two. First, in competitive analysis (a.k.a online algorithms) there is a state concept which is usually modeled as switching or movement cost. Second, in online algorithms one assumes that the cost vector for next round is known to the algorithm to make the decision; in contrast, in online learning, the decision maker first makes the decision for next round and after that observes the cost vector. One interesting questions in connecting these two setting would be adding the switching cost to the regret incurred by the online learner. More specifically, one may consider the 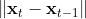as the movement cost at round t. Obviously, the decision maker needs to consider the switching cost in his decision to minimize it. Having this formulation, the learner competes with the best offline decision maker with bounded switching cost. When the bound on switching cost is in terms of number of rounds T, then we recover the standard setting of online learning. I will post more about this problem and some solutions soon, hopefully :-)

Stochastic Gradient Descent with only ONE Projection

With the increasing amount of data that is available for training, it becomes an urgent task to devise efficient algorithms for optimization/learning problems with unprecedented sizes. Online learning algorithms, such as celebrated Stochastic Gradient Descent (SGD) and its counterpart Online Gradient Descent (OGD), despite of their slow rate of convergence compared with the batch methods, have shown to be very effective for large scale and online learning problems, both theoretically and empirically. Although a large number of iterations is usually needed to obtain a solution of desirable accuracy, the lightweight computation per iteration makes SGD attractive for many large-scale learning problems. To find a solution within the domain $\K$ that optimizes the given objective function $f(\x)$, SGD computes an unbiased estimate of the gradient of $f(\x)$, and updates the solution %for complex domains, such as a positive semidefinite (PSD) cone in metric learning and bounded trace norm matrices in matrix completion by moving it in the opposite direction of the estimated gradient. To ensure that the solution stays within the domain $\mathcal{K}$, SGD has to project the updated solution into the $\K$ at {\it every iteration}. For complex domains, such as a positive semidefinite (PSD) cone in metric learning and bounded trace norm matrices in matrix completion, the projection step requires solving an expensive convex optimization, leading to a high computational cost per iteration and consequently making SGD unappealing for large-scale optimization problems over such domains. For instance, projecting a matrix into a PSD cone requires computing the full eigen-decomposition of the matrix, whose complexity is cubic in the size of the matrix. The question is can we somehow reduce the number of projection steps? Our recent work solves this problem and will appear in NIPS 2012.