Online Learning with a Partially Observable Future Cost

The main idea in proving regret bound for the Follow the Perturbed Leader (FPL) algorithm is as follows: first, we define the hypothetical leader which knows the future cost vector before prediction on round 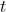which attains zero regret. Then we can prove that by adding some perturbation to the current cumulative cost vectors till time 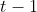the Player gets regret bound. Now the question is that if we have some partial information about future cost or we are allowed to query some information about the next round's cost, can we design algorithms with improved regret bounds. This problem is tackled down in two recent papers. In Online Learning with Prior Knowledge the authors proposed an algorithm which utilize such information as a kind of prior information. Recently in Online Learning with Queries a variant of Weighted Majority Algorithm with capability of querying limited information about the future cost vector is proposed.

No Free Experts, Hedging on Cost

Consider the following setting for learning from expert advice. In each round of the game between Player and Adversary, the player can ask for experts' suggestions but by paying some amount of money determined by each expert at the beginning of the round. In other words, at the beginning of each trial, the Player gets a cost vector which determines the cost of querying each expert for that round. Also let assume that Player has a budget constraint which would be for each round or long term constraint defined for all rounds. The goal of Player is to attain nontrivial regret bound under the budget constraint. Formally the Player tries to minimize and simultaneously satisfies the constraint .

The mentioned constraint is a long term constraint and we can alternatively define round based constraint as:.